When waves diffuse through a random medium, the mean free path is no longer the only length scale determining the physical situation. Due to interferences, additional effects will appear on the scale of the wavelength, lambda. A striking prediction made by Anderson in 1958 is that in fact diffusion should come to a halt in a medium where the mean free path is comparable with the wavelength. In the context of electronic systems, this has been used as an explanation for the transition from metallic to insulating behaviour with the addition of impurities. We study this phenomenon for the case of diffusing photons in a system made of particles with a high refractive index on the scale smaller than the wavelength of light. Here, localization can be observed without the complications induced by electron-electron, as well as electron-atom interactions, thus allowing a study of pure Anderson localization.
Since the discovery of the enhanced intensity in direct backreflection and thus the effects of weak localization [Wolf and Maret; van Albada and Lagendijk, Phys. Rev. Lett. 55, 2692 (1985)], it was tried to observe Anderson, or strong, localization of light. This is because light is a much better candidate for the observation of pure Anderson localization, where all effects are solely due to scattering and interference [Anderson, Phys. Rev. 109, 1492 (1958)]. However, due to the fact that very strongly scattering particles are needed to come close to the Ioffe-Regel criterion, progress has been slow over the course of the last twenty years. In addition, the problem is complicated by the fact that many measures of localization are ambivalent. In particular, measurements involving total intensities (in transmission or reflection) cannot distinguish between localization and absorption, as both lead to an exponential decrease in the number of transmitted photons.
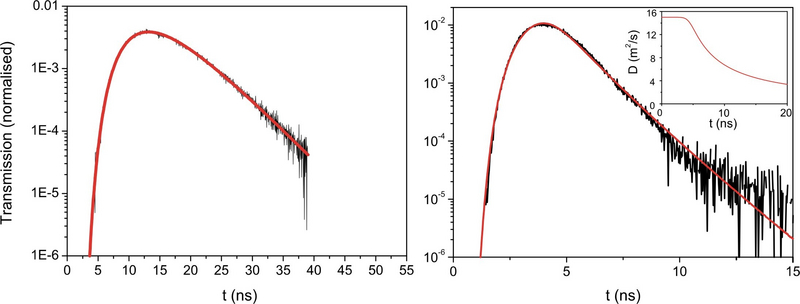
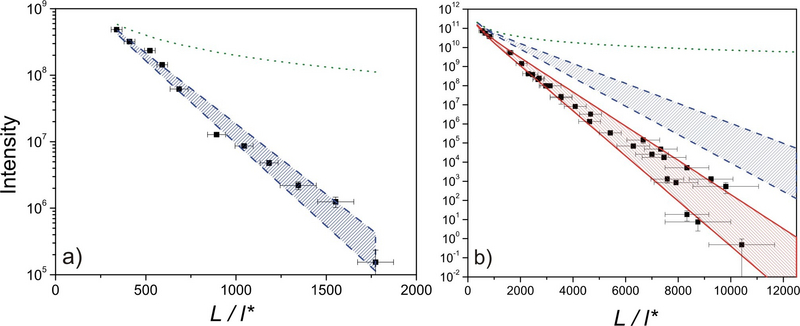
Time-resolved measurements in contrast can specifically look for long paths, where localization should occur and thus test for the hypothesis of a scale dependent diffusion coefficient. We carry out measurements of time-resolved transmission of a picosecond pulse through a multiple-scattering sample. For samples with very high turbidity (characterized by a low value of the mean free path l* - and measured from the width of the coherent backscattering cone), we observe increasing deviations from the behaviour of classical diffusion of a light-pulse [Stoerzer et al. Phys. Rev. Lett. 96, 063904 (2006)]. This indicates that the transport of light is slowed down for samples on very long paths, where the probability of closed loops is higher. These data can be well fitted with a time-varying diffusion coefficient, which is proportional to 1/t. In the diffusion picture, this translates to the statement that the spread of the photon cloud comes to rest at a certain point, which we identify with the localization length. With a measure of l*, the absorption length and the localization length, it is now also possible to gain information from static transmission measurements. While a combination of diffusion and absorption well describes the transmission through a sample with a value of kl*= 25, it fails to describe a sample with kl* = 2.5. When including the localization length however, good agreement with the data is found over 12 decades without any adjustable parameters.
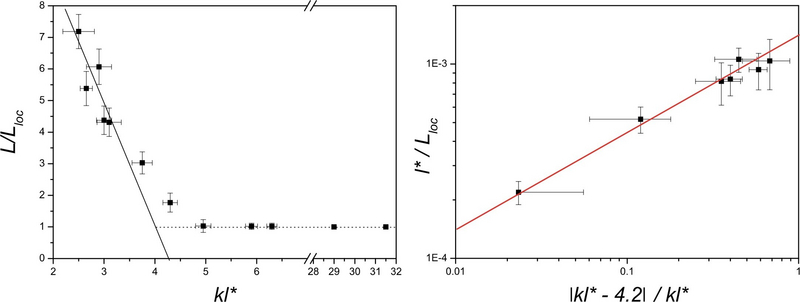
The determination of the localization length from time-resolved measurements allows the first determination of the critical exponent of localization, which has been studied with numerical simulations or a one-parameter scaling theory. While the results are in reasonable agreement with the scaling theory, they disagree with the numerical results, which predict a value of 1.5 in contrast to the experimental value close to 0.5 [Aegerter et al., Europhys. Lett. 75, 562 (2006)].
In order to demonstrate the interference nature of the observed effects, we are building up experiments to break time reversal symmetry on closed loops by the Faraday effect. Due to the rotation of the polarization in a strong magnetic field, counter-propagating photons will no longer be able to interfere, leading to the destruction of Anderson localization. In the case of weak localization as shown by the coherent backscattering cone, this has already been shown [Erbacher et al., Europhys. Lett. 21, 551 (1993)].
